Liens entre mathématiques et musique : l'exemple de Pierre Boulez

Pendant longtemps la musique fut considérée comme une science au même titre que l’astronomie ou la géométrie. Parmi les nombreux mathématiciens qui se sont penchés sur les problèmes musicaux on peut citer par exemple Pythagore (580 av. J.-C. - 495 av. J.-C.), Galilée (1564-1642) , Descartes (1596-1640) ou Euler (1707-1783). Voyons donc en quoi Arnold Schönberg (1874-1951), Iannis Xenakis (1922 - 2001) ou Pierre Boulez (1925-2016) ont révolutionné la musique.

Depuis les temps très anciens, Il est admis que deux sons joués ensemble, simultanément ou l’un après l’autre, donnent une impression harmonieuse. Cependant Pythagore  fut celui qui lança l’idée que la musique pouvait s’"expliquer mathématiquement".  La légende raconte qu’il découvrit le lien entre la musique et les nombres, au détour d’une promenade, en passant devant une forge. Il remarqua que la note produite par le marteau lorsqu’il frappe l’enclume ne dépend que de la masse de celui-ci. Plus le marteau est léger, plus le son est aigu. Dans un langage moderne, la fréquence de la note est inversement proportionnelle à la masse du marteau. En soupesant les marteaux, Pythagore s’aperçut que l’intervalle entre deux notes ne dépendait que du rapport entre leurs masses. Cette simplicité vint conforter les pythagoriciens que l’Univers était régi par les nombres.  Pour eux la musique était « l’art du nombre rendu audible » et donc classée parmi les sciences (voir ici, là ou  là).

Les pythagoriciens ont proposé une échelle musicale avec des intervalles constants. Un gros avantage est de pouvoir changer la note de départ sans altérer la gamme : la gamme de do et la gamme de sol sont rigoureusement identiques. Sans rentrer dans les détails ici cette gamme ne prend pas du tout en compte l'harmonie. Il y a donc eu un long travail pour proposer la gamme actuelle au XVIIIè siècle (voir ici pour plus de détails).  On parle de gamme tempérée :

 La valeur ¹² √d est appelée le demi-on chromatique.

A partir de la fin du XIXe siècle la musique savante occidentale connaît une véritable révolution. Les artistes de la Seconde école de Vienne (ici ) comme Arnold Schoenberg, Alban Berg (1885-1935) ou Anton Webern (1883-1945), s’élèvent contre le « diktat » de la tonalité, c'est-à-dire le principe d'une musique basée sur des accords et leurs successions. Si on analyse une œuvre (classique, variété, rock, etc..), on remarque que les fréquences d’apparition  des notes de la gamme varient fortement. et ont donc un rôle plus important. C’est une caractéristique de la musique tonale. Pour tourner le dos définitivement à la musique tonale, Arnold Schoenberg invente le sérialisme. La brique de base d’une pièce est une suite de douze sons où chaque note de la gamme chromatique est utilisée exactement une et une seule fois. L'ordre des douze sons est libre mais l’œuvre est  atonal car tous les sons sont autant représentés. On peut donc parler de « démocratie » sonore contre « tyrannie de la dominante ».

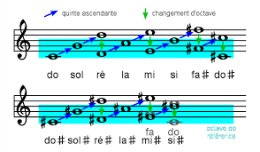
De manière pratique, on commence par associer à chaque note de la gamme tempérée un nombre entre 0 et 11.

Ensuite il faut choisir une permutation. Par exemple S = 10  0  6  7  5  1  4  2  3 11  9  8. On peut ensuite continuer soit avec la série miroir (12-S = 2 12  6  5  7 11  8 10  9  1  3  4) ou la série dans l'autre sens (S' = 8  9 11  3  2  4  1  5  7  6  0 10) ou bien en ajoutant k tons (par exemple S+2 = 0  2  8  9  7  3  6  4  5 1 11 10)

Parmi les plus connus des élèves de l'école de Vienne il y a Olivier Messiaen (qui a généralisé la notion de suite non seulement aux notes mais au rythme, à l'intensité aux attaques) et Pierre Boulez (resp. à gauche et à droite sur la photo ci-dessus). On assiste à l'arrivée d'un formalisme en musique qui prend tout son sens avec l'arrivée de la musique assistée par ordinateur. L'idée de mathématiser la musique a donc une très longue histoire dont la musique sérielle est une étape. Étape qui vient de perdre l'un de ses grands noms.