Espace de Minkowski

Lien pour voir article source de Wikipédia .

Géométrisation de la physique relativiste

Le cône de lumière de l'évènement e0.La flèche rose montre la dimension temporelle et les flèches grises, les dimensions spatiales.

Le cône de lumière de l'évènement e₀.
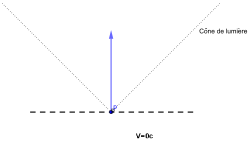
La flèche rose montre la dimension temporelle et les flèches grises, les dimensions spatiales.

Les points géométriques représentent les événements physiques et sont repérés par quatre coordonnées (ct,x,y,z) : la coordonnée de temps et les trois coordonnées d'espace. Les repères mathématiques y représentent les référentiels galiléens, et l'obligation en mathématiques de choisir un repère, pour désigner les points par des coordonnées, correspond à celle, en physique, de choisir un référentiel pour l'observateur, y compris pour le choix de la mesure du temps.

La particularité mathématique de cet espace affine tient à sa distance entre deux points, appelée pseudo-métrique, qui a été construite par Hermann Minkowski pour être invariante par les changements de repère que sont les transformations de Lorentz. La pseudo-métrique est aussi appelée pseudo-norme quand on utilise que l'espace vectoriel sous-jacent à l'espace affine. Cette pseudo-métrique correspond au temps propre entre deux événements qui peuvent être causalement joints, ou correspond à la distance propre entre eux s'il ne le peuvent pas.

La pseudo-métrique, notée $Δ s$ , est définie par $Δ s 2 = - c 2 (Δ t) 2 + (Δ x) 2 + (Δ y) 2 + (Δ z) 2$ ou $Δ s 2 = c 2 (Δ t) 2 - (Δ x) 2 - (Δ y) 2 - (Δ z) 2$ suivant la convention de signes $( - ; + ; + ; + )$ ou $( + ; - ; - ; - )$ choisie^[2]. Cette définition rend la pseudo-métrique identique à l'intervalle d'espace-temps qui est l'invariant relativiste par changement de référentiel galiléen.

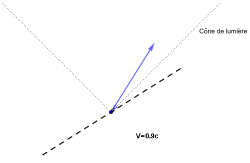
Un événement étant donné, l'ensemble des événements physiquement joignables dans le futur et de ceux du passé à partir desquels on pouvait joindre l'événement donné, forme un cône dans l'espace de Minkowski, appelé cône de lumière, et permettant des raisonnements purement géométriques par des dessins appelés diagrammes de Minkowski.

Dans cet espace, la dimension relative au temps peut être considérée comme un nombre imaginaire, alors que les trois autres coordonnées (spatiales) sont toujours des nombres réels : ce choix modifie l'écriture de la pseudo-norme et la présentation des calculs, sans apporter plus de simplicité.

Structure algébrique

L'espace de Minkowski étant un espace affine de dimension quatre, il est doté d'un point O (l'origine du repère) et d'un espace vectoriel de dimension quatre (sur $\R$ ).

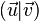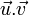L'espace vectoriel est doté d'une forme bilinéaire, notée $(\vec u | \vec v )$ ou $\vec u . \vec v$ , qui n'est pas un produit scalaire car elle n'est pas définie positive (ni définie négative) : on suppose qu'il existe une base vectorielle 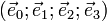$(\vec e_0 ; \vec e_1 ; \vec e_2 ; \vec e_3)$ telle que $(\vec u | \vec v )\, =\, u^0.v^0-u^1.v^1-u^2.v^2-u^3.v^3$ ^[3], où $\vec u = u^0.\vec e_0+u^1.\vec e_1+u^2.\vec e_2+u^3.\vec e_3$ .

Comme pour toute forme bilinéaire, il lui correspond une forme quadratique (qui est le carré de la pseudo-norme) : $(\vec u | \vec u) \, =\, (u^0)^2-(u^1)^2-(u^2)^2-(u^3)^2$

La matrice associée à cette forme bilinéaire, dans la base considérée ci-dessus, est 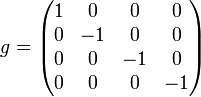$g = \begin{pmatrix}1&0&0&0\\0&-1&0&0\\0&0&-1&0\\0&0&0&-1\end{pmatrix}$ , on a donc $(\vec u | \vec v )\, =\,^{t}\vec u . g . \vec v$ , en écriture matricielle.

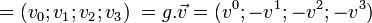L'écriture tensorielle permet d'introduire la convention de sommation d'Einstein : en définisant les « coordonnées contravariantes » $\ = (v^0;v^1;v^2;v^3)$ et les « coordonnées covariantes » $= (v_0;v_1;v_2;v_3) \;= g . \vec v = (v^0;-v^1;-v^2;-v^3) \;~$ , on écrit alors $\; \vec u . \vec v \; = \; u_i.v^i \; = \; u^i.v_i$

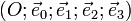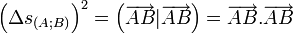L'espace affine est alors doté d'une distance particulière^[4] $\Delta s_{(\; ; \;)}$ souvent appelée pseudo-métrique, définie dans le repère $(O; \vec e_0 ; \vec e_1 ; \vec e_2 ; \vec e_3)$ par $\left( \Delta s_{(A;B)} \right)^2=\left( \overrightarrow{AB}|\overrightarrow{AB} \right) = \overrightarrow{AB}.\overrightarrow{AB}$ .

L'ensemble des transformations affines de l'espace de Minkowski qui laissent invariante la pseudo-métrique^[5] forme un groupe nommé groupe de Poincaré dont les transformations de Lorentz forment un sous-groupe.

Faire de la physique

Orienter l'espace et le temps

La structure algébrique seule ne permet pas de faire de la physique, il faut pour cela au moins : introduire le principe de causalité qui impose que l'on ne peut physiquement rebrousser le cours du temps ; postuler qu'un changement physique de référentiel galiléen ne peut changer l'orientation de l'espace tridimensionnel.

Ces contraintes physiques obligent à écarter 75% des éléments du groupe de Poincaré pour ne garder que ceux qui représentent un changement de référentiel réaliste : les translations et les transformations de Lorentz propres et orthochrones.

Ligne d'univers

Article détaillé : Ligne d'univers.

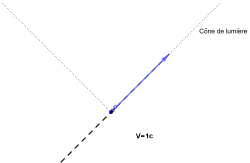
La trajectoire spatio-temporelle d'un corps ponctuel massif, appelée sa ligne d'univers, est une courbe dans l'espace de Minkowski ; mais toute courbe ne peut pas prétendre être une trajectoire réaliste (ligne d'univers) : elle doit pour cela toujours aller dans le sens croissant du temps et être entièrement contenue à l'intérieur de chacun des cônes de lumière centrés en chacun de ses points successifs (on dit alors qu'elle est de "genre temps") ; sinon cela signifie que la vitesse de la lumière est atteinte ou dépassée au point où cette condition n'est pas respectée. La trajectoire d'un corps ponctuel de masse nulle (un photon par exemple) est une ligne d'univers contenue dans le bord du cône de lumière, cette trajectoire étant rectiligne en général.

Comme toute courbe, une ligne d'univers peut être paramétrée, le paramètre n'étant pas obligatoirement doté d'un sens physique, mais tout observateur plongé dans cet espace-temps doit y avoir accès : n'oublions pas que l'espace de Minkowski représente notre espace dans lequel le physicien se trouve. 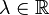Les coordonnées du corps M s'écrivent alors $\ M(ct(\lambda);x(\lambda);y(\lambda);z(\lambda))$ , où $\lambda \in \R$ est le paramètre.

Pour l'observateur, le choix du temps de son référentiel comme paramètre est le plus naturel : les coordonnées du corps M s'écrivent alors $\ M(ct;x(t);y(t);z(t))$ . Avec ce choix, qui est le plus accessible à l'observateur et utilisé en physique classique, la vitesse s'exprime $\ V(c;\dot x;\dot y;\dot z)$ , et n'est pas un quadrivecteur : sa pseudo-norme est variable par changement de référentiel. Par ce choix, pratique, l'observateur n'utilise pas les caractéristiques de l'espace de Minkowski.

Quadri-vitesse

Article détaillé : Quadrivecteur.

Géométrie dans l'espace de Minkowski

La géométrie dans l'espace de Minkowski présente un certain nombre de différences avec la géométrie dans un espace euclidien. Elle possède également des significations physiques précises.

Orthogonalité

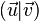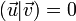Un espace de Minkowski possède une notion d'orthogonalité définie par la forme bilinéaire $(\vec u | \vec v)$ . Deux vecteur sont dit orthogonaux dans l'espace de Minkowski si et seulement si $(\vec u | \vec v ) = 0$ .

La notion d'orthogonalité est importante dans l'espace de Minkowski, car le complément orthogonal de la direction (tangente) d'une ligne d'univers en un point p est un "plan" tridimensionnel contenant tous les événements simultanés à l'événement p. En quelque sorte, il s'agit de prendre le "complément orthogonal du temps propre de cette ligne d'univers", ce qui donne - par définition de l'orthogonalité - l'ensemble des points qui n'ont aucune composante temporelle ( $Δτ = 0$ dans le référentiel galiléen tangent à la ligne d'univers), et qui sont donc "au même instant" que l'événement p pour cette ligne d'univers. Cet espace tridimensionnel est nommé plan de simultanéité pour cet événement sur cette ligne d'univers.

On voit bien qu'il n'est pas possible de prendre le complément orthogonal d'un simple point (événement) p sans lui associer sa ligne d'univers et donc sa vitesse. Cela illustre bien que - en relativité restreinte - la notion de simultanéité dépend de la vitesse.

Dans la représentation qu'est un diagramme de Minkowski, l'orthogonalité minkowskienne possède une propriété que ne possède pas l'orthogonalité euclidienne : l'angle entre un vecteur et son orthogonal varie en fonction de l'inclinaison du vecteur (en géométrie euclidienne, l'angle est fixe et égal à 90°). Quand le vecteur est de "genre lumière", ce vecteur est alors son propre orthogonal : la ligne d'univers est contenue dans le plan de simultanéité. Pour un photon, le temps de s'écoule pas quand il progresse sur sa ligne d'univers.

Détails mathématiques

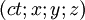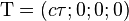Dans le référentiel tangent à cette ligne d'univers, les coordonnées sont $\ (ct;x;y;z)$ et $\ \Tau=(c\tau;0;0;0)$ est un quadrivecteur temps propre ou encore un quadrivecteur tangent à la ligne d'univers (du fait qu'il n'indique aucune séparation spatiale avec le référentiel tout en ayant une évolution temporelle car $\ \tau \ne 0$ par hypothèse).

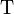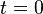Si un quadrivecteur $\ U=(ct;x;y;z)$ est perpendiculaire à $\ \Tau$ , on a : $Τ. U = c 2 τ. t - 0. x - 0. y - 0. z = τ. t = 0$ . Comme $\ \tau \ne 0$ , on a $\ t=0$ . Donc un point joint à l'origine de ce référentiel par un quadrivecteur $\ U$ orthogonal à la ligne d'univers représente un événement simultané avec celui de l'origine du référentiel (le décalage de temps est $\ t =0$ ).

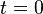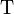Comme la forme bilinéaire est invariante par changement de référentiel, l'orthogonalité est assurée quelque soit le référentiel d'où on considère les quadrivecteurs, et ainsi dans les diagrammes de Minkowski, si l'angle dessiné entre $\ U$ et $\ \Tau$ dépend du référentiel choisit, leur orthogonalité minkowskienne est conservée.

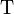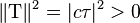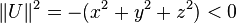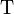Les calculs des carrés des pseudo-normes de $\ U$ et $\ \Tau$ , à l'aide des coordonnées dans le référentiel galiléen tangent, donnent : $\| \Tau \|^2 = | c\tau |^2 >0$ et $\|U\|^2 = - (x^2+y^2+z^2) < 0$ . Donc $\ \Tau$ est à l'intérieur du cône de lumière et $\ U$ est à l'extérieur. Par ailleurs, on sait que le carré de la pseudo-norme est conservé par changement de référentiel, donc ces caractéristiques restent vraies pour tout référentiel, et y compris dans les diagrammes de Minkowski.

Inégalité triangulaire

Paradoxe des jumeaux dans un espace de Minkowski

Dans un plan euclidien, l'inégalité triangulaire est la relation selon laquelle, quel que soit un triangle ABC, alors les longueur AB, BC et AC vérifient l'inégalité :

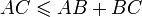$AC \leqslant AB + BC$ .

L'égalité a lieu quand les points A, B et C sont alignés. Cette inégalité signifie que dans l'espace euclidien, le trajet le plus court entre deux points est la ligne droite.

Dans l'espace Minkowskien, il existe un équivalent de l'inégalité triangulaire, établissant les relations entre les longueurs des côtés d'un triangle. Toutefois, celle-ci n'est cohérente que si le triangle est entièrement compris dans un cône de lumière, et si AB, BC et AC sont orientés vers le futur.

Pour un triangle ABC vérifiant ces conditions, on a alors l'inégalité dans l'espace Minkowskien :

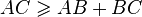$AC \geqslant AB + BC$ .

Cette inégalité est l'inverse de celle de l'espace euclidien. Dans l'espace Minkowskien, un chemin faisant un détour (dans l'espace-temps) est toujours plus "court" (en terme d'intervalle espace-temps) que la "ligne droite". Une "ligne droite" dans l'espace Minkowskien est la ligne d'univers d'une particule qui n'est soumise à aucune force, donc à vitesse constante ou stationnaire.

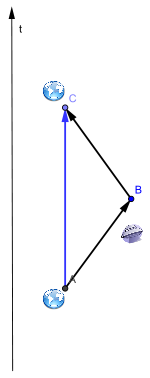
Cette propriété permet d'illustrer et d'expliquer le paradoxe des jumeaux en relativité restreinte. Le "jumeau" restant sur terre parcourt une "ligne droite" dans l'espace-temps AC. Le jumeau qui voyage parcourt deux segments de droites AB et BC (il fait demi-tour en B pour rejoindre sont jumeau en C). Les lignes d'univers des deux jumeaux forment un triangle ABC, dont les côtés sont de genre temps (vitesse des jumeaux inférieure à celle de la lumière) et orientés vers le futur.

L'intervalle espace-temps du jumeau qui voyage est donc inférieur, selon l'inégalité triangulaire Minkowskienne, à celui du jumeau stationnaire. Le temps propre du jumeau qui voyage est donc inférieur, et il est donc plus jeune au terme de son voyage que son jumeau resté sur Terre.

On voit que ce raisonnement utilise implicitement la propriété suivant laquelle, dans l'espace de Minkowski, « par deux points distincts passe une et une seule droite ».

Géométrie hyperbolique

Notes

Par exemple, la causalité est une hypothèse physique indépendante qu'il est nécessaire d'ajouter si on veut identifier l'espace de Minkowski à l'espace physique.
↑ La convention $( - ; + ; + ; + )$ correspond au choix fait dans les textes anglo-saxons ; la convention $( + ; - ; - ; - )$ correspond au choix fait dans les célèbres textes pédagogiques de Lev Landau, par exemple. Ce dernier choix est considéré comme "plus physique" par Roger Penrose car la métrique est positive pour les lignes d'univers de genre temps, qui sont les seules admises pour des particules massives.
↑ Avec la signature $( + ; - ; - ; - )$
↑ Elle ne répond pas à la définition mathématique de distance , mais joue un rôle similaire à la distance dans un espace affine euclidien.
↑ Parmi la pseudo-métrique, la forme bilinéaire et la pseudo-norme, si l'une est laissée invariante par une transformation de l'espace alors les deux autres aussi sont invariantes.

Voir aussi

[0] Par exemple, la causalité est une hypothèse physique indépendante qu'il est nécessaire d'ajouter si on veut identifier l'espace de Minkowski à l'espace physique.

[1] La convention $( - ; + ; + ; + )$ correspond au choix fait dans les textes anglo-saxons ; la convention $( + ; - ; - ; - )$ correspond au choix fait dans les célèbres textes pédagogiques de Lev Landau, par exemple. Ce dernier choix est considéré comme "plus physique" par Roger Penrose car la métrique est positive pour les lignes d'univers de genre temps, qui sont les seules admises pour des particules massives.

[2] Avec la signature $( + ; - ; - ; - )$

[3] Elle ne répond pas à la définition mathématique de distance , mais joue un rôle similaire à la distance dans un espace affine euclidien.

[4] Parmi la pseudo-métrique, la forme bilinéaire et la pseudo-norme, si l'une est laissée invariante par une transformation de l'espace alors les deux autres aussi sont invariantes.

[2]

[3]

[4]

[5]