Wakan Tanka pour les Sioux, Mulungu pour les Bantous, l'Éternel Ciel bleu pour les Mongols, YHWH, Allah, Odin, Brahma… Depuis la nuit des temps, quel que soit le nom qui lui est donné, les croyants en parlent avec ferveur, les athées avec conviction, les agnostiques avec distance. Christoph Benzmüller est le premier à pouvoir l'affirmer avec certitude : "Dieu, dans sa définition la plus répandue en métaphysique, existe nécessairement. On ne peut penser un monde dans lequel il n'existerait pas." Cette assurance, ce chercheur de l'université de Berlin la tire des mathématiques, et de leur cœur même, la logique. Mieux : il la fonde sur la capacité de l'informatique à valider sans erreur possible les démonstrations. Parachevant des siècles de réflexions métaphysiques, son logiciel a vérifié la justesse de l'argument ontologique selon lequel l'existence de Dieu est nécessaire à tout système de pensée logique. Et l'ordinateur a parlé : "L'énoncé 'Dieu existe' est une proposition vraie au sens logique et mathématique", assène Christoph Benzmüller.

Précisons que sa démarche n'est pas portée par la foi. "Ce travail n'a pas pour but de servir une quelconque religion - aucun non-croyant ne se laissera d'ailleurs convaincre par une formule mathématique. Non, ce qui est intéressant, c'est d'investiguer la cohérence d'un concept, qu'on l'appelle Dieu ou non. Cela permet d'en apprendre plus sur les croyances qui y sont rattachées." Ajoutons que cela ne concerne pas un Dieu à l'apparence définie - vieux, barbu et sage, bien souvent - ni un être dont la nature engendre forcément une action, tantôt créatrice, tantôt destructrice. "Cette démonstration prouve l'existence logico-mathématique d'une entité abstraite présentant certaines propriétés, mais pas celle qui déclenche l'amour, et encore moins le fanatisme", commente Shahid Rahman, mathématicien et philosophe à l'université de Lille.

La démarche n'est pas portée par la foi. Le théorème n'affirme pas que Dieu existe réellement. Juste qu'il est irrationnel de dire qu'il n'existe pas

Soulignons surtout que ce travail ne valide pas la pertinence de la foi, mais sa cohérence. Le théorème n'affirme pas que Dieu existe réellement. Juste qu'il est irrationnel de dire qu'il n'existe pas. Ce qui, en soi, est déjà renversant… Cette analyse des structures logiques de nos croyances permet de voir cette figure qui berce depuis toujours l'humanité - qui la hante, diraient d'autres - dans toute sa singularité. C'est un fait : que l'on y croie ou pas, Dieu a un statut bien supérieur aux autres entités peuplant notre esprit.

Prenez la licorne. Cette sorte de cheval cornu, apparu durant l'Antiquité, continue à vivre à travers la littérature et l'imaginaire enfantin. Certes, son existence n'est pas impossible - aucun principe évolutif n'interdit la sélection naturelle d'un tel animal. Mais tout esprit adulte et raisonnable est amené à penser que c'est un être totalement imaginaire. Il n'en va pas de même pour Dieu. L'argument ontologique le démontre : son existence dans notre esprit n'est pas seulement possible, mais nécessaire. Croire en Dieu, ce n'est donc pas comme croire aux licornes. Le concept a toujours  été là, présent dans la nature avant même qu'on ne le formalise, à la manière du théorème de Pythagore. Contrairement à notre cheval cornu, aux lutins et autres trolls, Dieu n'est pas né de l'imagination, mais de la logique. "Il y a une différence fondamentale entre un objet imaginaire comme la licorne et Dieu : l'être d'une licorne inclut des contradictions, alors que les propriétés de l'être divin dont l'existence est ici démontrée n'en présentent aucune, dans les conditions de la logique", souligne Baptiste Mélès, chercheur en logique et philosophie de l'informatique au CNRS.

UNE QUÊTE PHILOSOPHIQUE

Cela fait plus de mille ans que cette nécessité de l'existence divine est pressentie. Si les prémisses en sont attribuées au philosophe latin Boèce, c'est la formulation du moine bénédictin du XIe siècle Anselme de Cantorbéry qui rend l'entreprise célèbre (voir p. 72-73). Que d'encre elle a fait couler ! Elle a été retravaillée par Descartes, Hegel et Leibniz, débattue par Pascal, Kant et Spinoza, mais elle a toujours tourné autour d'un argument à la simplicité déconcertante : "Dieu a toutes les perfections, or l'existence est une perfection, donc Dieu existe."

Plus littéraires que logiques, de tels arguments peuvent sembler du domaine de la discussion philosophique, bien loin d'une approche logico-mathématique. C'est sans compter Kurt Gödel. Ce pur logicien est célèbre pour avoir prouvé, au début des années 1930, qu'il existe des vérités mathématiques non démontrables. Jusqu'alors, on pouvait croire que toute difficulté était surmontable. Eh bien non ! En s'appuyant sur le langage formel de la logique moderne, le mathématicien autrichien démontre que certaines vérités ne peuvent être atteintes. Auréolé d'un prestige inégalable, Kurt Gödel commence à travailler sur la fameuse preuve ontologique à partir des années 1940, d'abord à Vienne, puis à Princeton, aux États-Unis.

Car contrairement à ce prédisait Kant, qui déclarait "close et achevée" la logique philosophique traditionnelle, celle-ci n'a en fait jamais cessé d'évoluer et s'est même métamorphosée à la fin du XIXe siècle, après son union avec les mathématiques formelles. Le mathématicien allemand Gottlob Frege a notamment conçu, en 1879, un des premiers langages formalisés qui permettent de vérifier un raisonnement philosophique de la même manière qu'un calcul arithmétique. Suivi, en 1910, par le logicien américain Clarence Lewis, dont la logique modale explose au cours des décennies suivantes. "Des concepts tels que 'nécessité' ou 'possibilité', utilisés en théologie et en logique, acquièrent alors la respectabilité attachée à la calculabilité ou à tous les objets calculables, qui font autorité dans le milieu des sciences", commente le philosophe Frédéric Nef. Kurt Gödel s'attache donc à traduire Dieu dans ce langage de la logique modale, suivant les règles du système logique K.

"En termes de rigueur, ce sont les moins suspectes car elles répondent au plus grand nombre de contraintes logiques", souligne Baptiste Mélès. Gödel s'inspire des raisonnements théologiques de Leibniz, précurseur de ces langages modernes, notamment de son concept de "perfections", qu'il transforme en "propriétés positives" - Dieu est alors défini comme celui qui les possède toutes. Il cherche les meilleurs axiomes, les postulats les plus minimalistes et féconds. Et, après des décennies de travail solitaire, il finit par être satisfait de son résultat.

L'énoncé 'Dieu existe' est une proposition vraie au sens logique et mathématique - CHRISTOPH BENZMÜLLER, Chercheur en philosophie et mathématiques à l'université de Berlin

Sa preuve ontologique circule pour la première fois en 1970 dans les couloirs de son université : 12 lignes cabalistiques contenant 5 axiomes, 3 définitions, 3 théorèmes et 1 corollaire (voir p. 71), menant à la conclusion que le mathématicien, selon la légende, aurait résumée à sa mère avec ces quelques mots tendres sur une carte postale : "Maman, tu vas être contente, Dieu existe !" Cette démonstration sera publiée officiellement en 1987, neuf ans après sa mort.

UN LOGICIEL INFAILLIBLE

Sauf qu'elle n'a pas mis fin à l'interminable débat commencé quinze siècles plus tôt… Si simple, concise et élégante soit-elle, elle a été âprement mise en doute et même modifiée par différents logiciens, en particulier sur le choix des axiomes, mais aussi l'exactitude de la preuve. C'est que, en logique, chaque étape apporte quantité de sous-problèmes plus complexes les uns que les autres. "De nombreuses théories manquent de précision, pointe Christoph Benzmüller. Car une hypothèse repose en grande partie sur l'intuition du chercheur. Et à l'époque de Gödel, certaines vérifications exigeaient un temps et une méthode encore hors de portée." Comme un nouveau pied de nez de la part d'une entité qui semble devoir rester inaccessible, le débat paraissait condamné à s'éterniser…

C'est là qu'interviennent les travaux de Christoph Benzmüller, spécialiste des outils de vérification automatique des preuves mathématiques. Ces logiciels qui permettent de valider chacune des étapes des raisonnements sont devenus ultra-puissants. "Grâce aux outils informatiques, nous pouvons vérifier la cohérence d'une proposition logique en très peu de temps", acquiesce le chercheur. À la croisée de la logique traditionnelle, des mathématiques et de l'informatique, le chercheur trace avec Edward Zalta, de l'université Stanford, les contours d'une nouvelle discipline : la métaphysique computationnelle, "une première étape dans la construction d'une inter face entre systèmes informatiques et concepts métaphysiques". En 2013, son logiciel, Leo-II, est fin prêt. Le rêve du philosophe allemand Gottfried Wilhelm Leibniz de faire de la logique un calcul algorithmique mécaniquement décidable n'est plus hors de portée. Et quel meilleur baptême que de se confronter au plus métaphysique de tous les concepts ?

LA MORT DU LIBRE ARBITRE

Le chercheur commence par encoder dans son logiciel la preuve ontologique de Gödel, dans sa forme symbolique telle qu'elle est présentée sur le manuscrit d'origine. Il appuie sur une touche et, en quelques secondes, le résultat tombe : Gödel s'est trompé ! Le théorème est inconsistant, les axiomes ne tiennent pas, la conclusion "Dieu existe" n'est pas valide… Stupéfaction ! Pas un seul des nombreux philosophes, logiciens et mathématiciens qui avaient pourtant décortiqué le travail originel de Gödel n'avait décelé cette faille. "La machine vient pallier les limites de l'humain qui ne peut pas opérer autant de calculs", avoue Yann Schmitt, philosophe à l'université Paris-I-Panthéon-Sorbone. Mais pas de panique : au cours de l'histoire, plusieurs chercheurs ont légèrement reformulé le théorème de Gödel. En particulier Dana Scott, à qui le logicien avait permis de recopier sa démonstration de son vivant, et qui avait opéré un minuscule changement dans la huitième ligne. Avec son confrère Bruno Woltzenlogel-Paleo, Christoph Benzmüller insère ces quelques symboles dans Leo-II… qui valide la démonstration de l'existence nécessaire de Dieu. Gödel s'était à peine trompé !

Dans la foulée, le logiciel détecte un problème, déjà relevé par certains logiciens : la version de Dana Scott est juste, mais elle implique un effondrement modal. C'est-à-dire qu'elle demande d'accepter que tout ce qui existe existe nécessairement, que tout n'est que fatalité. Si vous possédez un vélo rouge, il ne pouvait en être autrement, jamais vous n'auriez pu posséder un vélo bleu à la place. Toute la subtilité de la logique modale, qui distingue le possible du nécessaire, s'écroule. Bref, Dieu existe, oui, mais pas le libre arbitre. Une telle conclusion ne convient pas à Christoph Benzmüller : "Certains chercheurs pensent que Gödel était satisfait de cet effondrement modal. Mais il me paraît incohérent d'utiliser un certain type de logique pour prouver un raisonnement, et d'admettre avec sa conclusion que cette même logique s'effondre."

AU FINAL, SEUL L'HUMAIN DÉCIDE

Le logicien se penche alors sur deux variantes de la théorie de Gödel. Celle développée dans les années 1990 par le philosophe Curtis Anderson, professeur à l'université de Californie, qui modifie le premier axiome de façon à ce que la négation d'une propriété négative, comme la fainéantise, ne donne pas forcément une propriété positive, instaurant le concept de propriétés "indifférentes". Et celle de Melvin Fitting, philosophe américain - qui reformule en 2002 le travail de Gödel dans un ordre supérieur de logique permettant de distinguer, par exemple pour le mot "chat", la désignation de celui de la voisine et celle de l'espèce en général. Christoph Benzmüller entre dans son logiciel de métaphysique computationnelle ces deux théorèmes reformulés. Et le résultat, publié il y a deux ans, est sans équivoque : ils sont validés, sans effondrement modal cette fois. Ouf ! le libre arbitre est préservé. La quête ontologique a atteint son terme.

Mais justement, en parlant de libre arbitre : que faire d'une telle vérité ? Ne reste-t-il plus qu'à admettre l'existence de ce Dieu logico-computationnel, non pas par foi, mais par raison ? "Il faut prendre ce travail hors normes avec un peu de distance, prévient Gérard Huet, logicien à l'Inria. 'Dieu existe, on en a une preuve' : c'est effectivement la conclusion de Gödel. Mais si l'on voulait être plus précis, nous devrions dire que 'l'union de toutes les essences positives est une notion cohérente'."

À ce titre, Dieu a un statut assez proche de concepts mathématiques dont la cohérence a été démontrée. "Celui de nombre réel est extrêmement fécond, mais pour autant, il me semble illusoire de chercher à savoir s'ils existent réellement", compare Olivier Gasquet, chercheur à l'Institut de recherche en informatique de Toulouse. Autrement dit, ce travail n'éclaire pas tant Dieu que l'idée que l'on s'en fait. "Il faut s'entendre sur la définition de départ, c'est-à-dire sur les axiomes logiques. Et cela, seul l'humain peut le décider. L'ordinateur ne peut pas, seul, aboutir à l'existence de Dieu", pointe Shahid Rahman.

Il existe des échappatoires, comme le rejet de la définition de départ de Gödel. On peut ne pas être d'accord avec la proposition "l'existence nécessaire est une propriété positive". Sans elle, Dieu disparaît ! "Mais le contraire est aussi possible, sourit Christoph Benzmüller. Si quelqu'un de profondément athée acceptait les axiomes et la logique, il serait irrationnel de sa part de ne pas en admettre la conclusion."

Les anthropologues, les neurologues, les psychologues avaient déjà avancé leurs arguments expliquant pourquoi l'humain est un animal de foi - c'est d'ailleurs le seul (voir p. 74). Ce travail de métaphysique computationnelle complète le tableau. Non pas que ce soit suivant un raisonnement conscient que les humains aient accédé à cette entité surplombant le monde de sa perfection. Mais la foi, et son incroyable universalité, a pu être influencée par cette nécessité de l'existence divine, inscrite dans la logique de la pensée. "Je pense en effet que ça a pu jouer un grand rôle, confirme Christoph Benzmüller. La cohérence d'un concept peut faciliter le fait d'y adhérer, même de façon inconsciente." Comme si parler, raisonner, c'était déjà faire exister Dieu. C'était déjà un peu y croire.

Plus de 6 humains sur 7 sont croyants

Judaïsme

Il se fonde sur un dieu unique, omniscient, omnipotent, omniprésent : YHWH.

Christianisme

Il transforme le dieu des juifs en une trinité : le Père, le Fils et le Saint-Esprit.

Islam

Il revient à un dieu indivisible, Allah, dont la révélation s'accomplit dans le Coran.

Religions dharmiques

Le Brahman et le dharma sont des principes qui peuvent s'incarner en déités.

Autres religions

L'animisme et le culte des ancêtres restent très présents dans de nombreuses sociétés.

Sans religion

Les athées refusent de croire en un dieu. Les agnostiques, eux, ne se prononcent pas.

Les religions se portent bien…

Tous cultes confondus, le nombre de fidèles dans le monde est en constante augmentation et devrait continuer sur cette lancée. Une évolution portée par une démographie dynamique.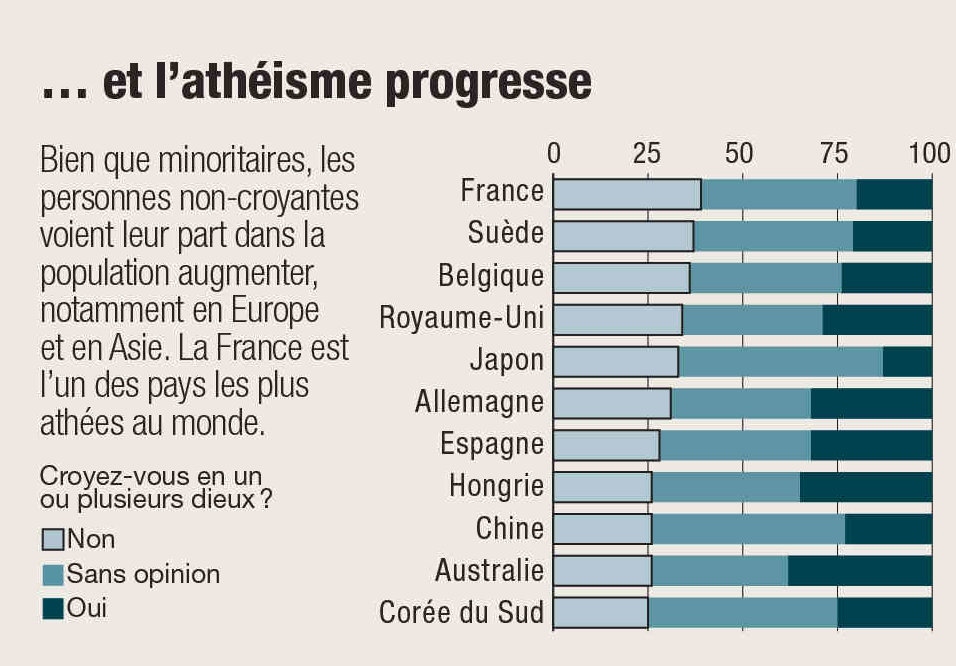

… et l'athéisme progresse

Bien que minoritaires, les personnes non-croyantes voient leur part dans la population augmenter, notamment en Europe et en Asie. La France est l'un des pays les plus athées au monde.

LA MÉTAPHYSIQUE COMPUTATIONNELLE MÊLE TROIS DISCIPLINES

Elle s'intéresse aux concepts de la métaphysique…

En particulier ceux de la théologie, où les divinités sont étudiées suivant un raisonnement logique, et non à travers une expérience mystique.

… dans le langage des mathématiques…

En particulier celui de la logique formelle, où le raisonnement et son interprétation sont énoncés à travers un calcul symbolique.

… en utilisant la puissance de l'informatique

En particulier les méthodes de vérification par ordinateur, qui permettent de s'assurer que chaque étape d'un raisonnement est juste, sans erreur possible.

Et le diable, dans tout ça ?

Si Dieu passe brillamment le test de l'existence, qu'en est-il de son satané antagoniste ? Nous avons soumis la question à Christoph Benzmüller, qui s'est amusé à la passer au crible de la métaphysique computationnelle : "Ajoutons à la démonstration qu'une propriété est négative si et seulement si elle n'est pas positive, et définissons une entité comme étant le diable si et seulement si elle possède toutes les propriétés négatives. "

En quelques millisecondes, le logiciel Leo-II a rendu sa conclusion : l'existence du diable n'est pas possible ! "' Être tel que l'on est' est une propriété positive, donc 'ne pas être tel que l'on est' est une propriété négative logiquement possédée par le diable. Or il ne peut exister d'entité qui n'est pas identique à elle-même", commente le chercheur.

L'EXISTENCE DE DIEU DÉMONTRÉE EN 12 ÉTAPES

1. Définition de Dieu

La démonstration commence par poser la définition de Dieu : être tel que Dieu signifie posséder toutes les "propriétés positives".

2. "Propriétés positives"

Ce premier axiome précise la notion de "propriété positive", inspirée de la notion de "perfection" de Leibniz : il pose qu'une propriété donnée, ou sa négation, est positive.

3. La positivité se transmet

Ce deuxième axiome pose que toute propriété engendrée par une propriété positive est aussi positive.

4. La positivité s'exprime

Ce premier théorème démontre que toute propriété positive est possiblement exemplifiée, c'est-à-dire exprimée par un être.

5. Être Dieu est positif

Ce troisième axiome pose qu'être tel que Dieu est une propriété positive.

6. Dieu est possible

Ce corollaire établit qu'être tel que Dieu est possiblement exemplifié. Autrement dit, Dieu est possible.

7. Nécessité des propriétés positives

Ce quatrième axiome pose que les propriétés positives le sont nécessairement.

8. Définition de l'essence

Ici est défini ce qu'est l'"essence" : une propriété "E" est l'essence d'un être si toutes les propriétés de cet être sont impliquées par "E". Dana Scott ajouta : et si cet être possède "E".

9. L'essence de Dieu

Ce second théorème établit qu'être tel que Dieu est l'essence de Dieu.

10. Nécessité de l'existence

Ici est définie l'existence nécessaire d'un être : c'est la nécessaire exemplification de son essence.

11. Exister nécessairement est positif

Ce cinquième et dernier axiome pose que l'existence nécessaire est une propriété positive.

12. Dieu existe

La conclusion s'impose : l'essence de Dieu est nécessairement exemplifiée. Autrement dit, Dieu existe.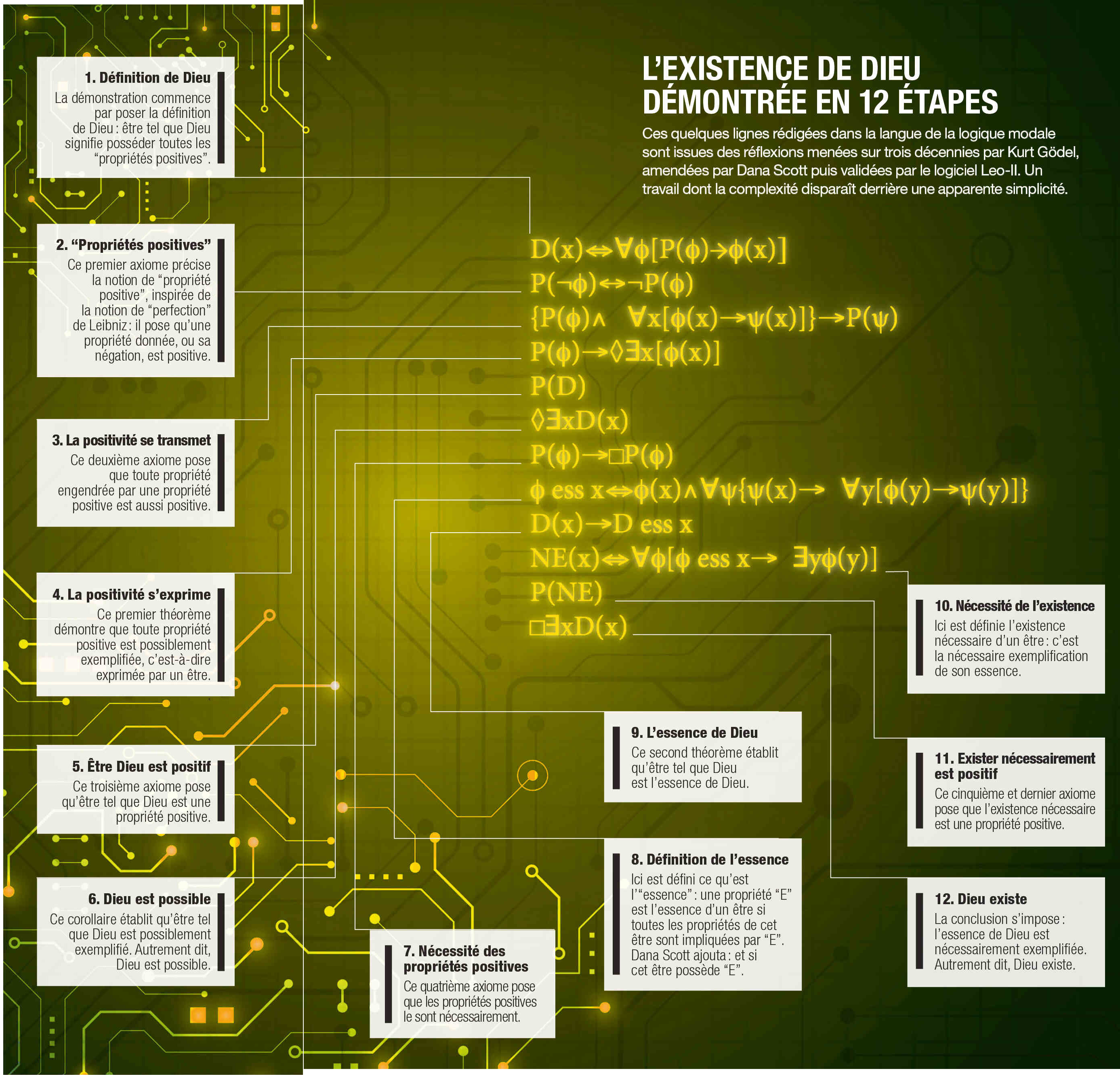

QUINZE SIÈCLES DE CHEMINEMENT POUR DÉMONTRER L'EXISTENCE DE DIEU

VIe

BOÈCE

Philosophe et homme politique latin, Boèce (480-524) est le premier à proposer un argument ontologique. En usant de la logique aristotélicienne, il écrit que "rien ne peut se penser de plus grand que Dieu" et conclut que la vision chrétienne de la nature divine est correcte.

XIe

ANSELME DE CANTORBÉRY

C'est la formalisation de saint Anselme de Cantorbéry (1033-1109) qui rend la preuve ontologique célèbre. S'inspirant des écrits de Boèce, ce moine bénédictin conclut en cinq propositions logiques que l'existence de Dieu ne peut pas se limiter au seul intellect, mais qu'il existe dans la réalité.

XVIIe

DESCARTES

Le philosophe et mathématicien français René Descartes (1596-1650) réduit l'argument à trois propositions. Surtout, il définit Dieu par le terme "parfait", et l'existence comme étant une propriété inhérente à la perfection, préfigurant ainsi les travaux de Leibniz et Godël.

XVIIIe

LEIBNIZ

La perfection telle que décrite par Descartes ne satisfait pas le philosophe allemand Gottfried Wilhelm Leibniz (1646-1716). Il la transforme en des perfections, que Dieu posséderait toutes. Dieu commence à être perçu comme un objet mathématique doté de propriétés.

1970

GÖDEL

Le logicien autrichien Kurt Gödel (1906-1978) transforme le concept de perfections en propriétés positives. Il écrit une démonstration de l'existence de Dieu en langage mathématique, celui de la logique modale.

2018

À l'aide de son logiciel de vérification des preuves mathématiques, l'informaticien Christoph Benzmüller valide des versions légèrement modifiées de l'argument ontologique de Gödel.

Kurt Gödel à l'université Princeton, en 1956.