In Brief

Physics and Mathematics are extremely important subjects. Actually, that’s a bit of an understatement.

Physics and Mathematics allow us to peer out into the cosmos and understand the inner workings of the universe. At once, they show us our insignificance and our remarkable potential; they give us a hint of the vast possibilities that exist—of what we could (and may) one day accomplish. They allow us to see the world and to see ourselves anew.

That begins to scratch the surface of these subjects.

No one can deny their importance; however, it is also a fact that many people don’t know where to begin investigating these topics…what books to study, what themes to begin with. On top of this, many feel intimidated by physics and math—they seem to think that they are things which only the sharpest individuals are able to understand.

But nothing could be farther from the truth.

True, these subject areas might not be the easiest that you will ever happen across, but they are far from impossible. So. If you want to be a physicist or a mathematician, or if you just want to understand the subjects, here’s where to start.

Huge thanks to the wonderful Moinak Banerjee for his work on this.

Physics

• Here is professor John Baez advice on how to learn physics and mathematics. He mentions the books you should read, and they are conveniently listed according to increasing levels of difficulty.
• This is the list of books that Berkeley recommends for people who want to teach themselves physics.
• And yet another list that is pretty good, which was compiled on Physics Stack Exchange.
• Nobel laureate professor Gerard ‘t Hooft has recommended some learning sources that are all free, and he also has advice related to how to earn your own Nobel prize.
• Here is some great advice from a physicist on Physics Forums regarding what you should do if you want to do more than just learn physics—on what to do if you want to actually have a career in physics.
• To supplement these, check out our extensive list of online physics lecture videos.

Math

• Mathematician Terence Tao, who is also a Fields medalist and a Breakthrough prize winner, gave some beautiful advice on pursuing a career in math here.
• If you are looking for mathematics books you should read, here is an extensive list by Berkeley.
• The aforementioned should probably be followed up by the compilation from the Math Stack Exchange.
• Also, there’s an extensive list of what you should read on the Georgia Institute of Technology website, and all of the texts that they link to are online and free.
• You can access more free math texts here and here.

Separating Science From Pseudoscience

• Here is a hilarious point system on how to tell if something is ‘crank science’ from John Baez.
• Warren Siegel has an equally hilarious write up here.
• And finally, from Gerard ‘t Hooft.

Now venture forth, live long, and study well.

by Ross Rhodes

N.B. Familiarity with The Reality Program Chapter 2 is assumed.

J ohn Archibald Wheeler is one of those thinkers who takes the ideas of quantum mechanics seriously. After studying the Copenhagen explanation of the double slit experiment â€" with its emphasis on what the observer knows and when it is known â€" Wheeler realized that the observer's choice might control those variables in a test. 

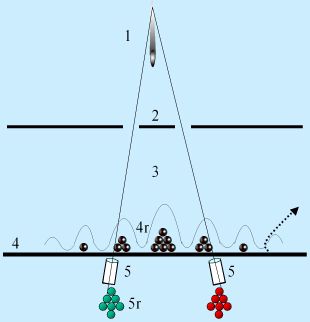
1. Photon (or other quantum unit) is sent toward double slit.

2. Photon passes through double slit unobserved, logically either through one, through the other, or through both. To obtain an interference pattern, we surmise that something must pass through both slits; to obtain a particle distribution, we surmise that the photon must pass through one or the other. Whatever the photon does, it presumably does it now when it passes through the slits.

3. After passing through the slits, the photon is in transit towards the back wall.

At the "back wall," we have available two separate methods of detecting the photon.

4. First, we have a screen (or other detection system that can measure the horizontal placement of a photon hit, but is not able to distinguish where the photon came from).

The screen can be removed, as indicated by the dotted line. It can be removed quickly, very quickly, after the photon has passed the double slits but before the photon reaches the plane of the screen. That is, the screen can be removed while the photon is in transit in region 3.

Or the screen can be left in place. This is the experimenter's choice, which is delayed until after the photon has passed the slits (2) in whatever manner it happens to do so.

5. If the screen is removed, we reveal two telescopes. The telescopes are tightly focused on, watching, observing, just the narrow space of one slit only. The left telescope watches the left slit; the right telescope watches the right slit. (The mechanism/metaphor of the telescope assures that if you are looking through the telescope, you will see a flash of light if the photon went either wholly or in part through the slit on which it is focused; otherwise not. Therefore, you will obtain "which-path" information about the photon hit.)

Now suppose we have a photon in transit in region 3. The photon has already passed the slits.

    We can yet choose to leave the screen in place, in which case we do not know which slit the photon went through.

    Or we can choose to remove the screen. If we remove the screen, we will expect to see a flash at one telescope or the other (or both, except that never happens) for every photon sent through. Why? Because the photon has to go through either one slit, the other slit, or both slits. Those are all the possibilities. By watching both slits, we must see one of the following:

• a flash at the left telescope and no flash at the right telescope, indicating that the photon went through the left slit; or
• a flash at the right telescope and no flash at the left telescope, indicating that the photon went through the right slit; or
• a weak half-flash at both telescopes indicating that the photon went through both slits.

Those are all the possibilities.

    Upon observation at the screen QM tells us what we will get: Pattern 4r, which is exactly reminiscent of wave interference caused by two symmetrical waves, one emanating from each of the slits.

    Upon observation at the telescopes QM tells us what we will get: Pattern 5r, which is exactly reminiscent of particle-like behavior traveling from the source, through one slit or the other, and being detected at the telescopes.

Consider the difference in the experimental set up depending on our choice of detection. If we choose to leave the screen in place, we get a particle distribution consistent with the interference pattern that would be produced by two hypothetical symmetrical waves, each emanating from one of the slits. We might say (although we are extremely reluctant to say this) that the photon traveled as a wave from the point of origin, through both slits, and on to the screen.

    On the other hand, if we choose to remove the screen, we get a particle distribution consistent with the clumping pattern that would be produced by particle motion from the point of origin through one slit or the other and to the left telescope or to the right telescope. After all, the particle "appeared" (we saw a flash) at one telescope or the other, rather than "appearing" at some other point along the length of the screen.

    In summary, we have chosen whether to know which slit the particle went through, by choosing to use the telescopes or not, which are the instruments that would give us the information about which slit the particle went through. We have delayed this choice until a time after the particles "have gone through one slit or the other slit or both slits," so to speak. Yet, it seems paradoxically that our later choice of whether to obtain this information determines whether the particle passed through one slit or the other slit or both slits, so to speak. If you want to think of it this way (I don't recommend it), the particle exhibited after-the-fact wave-like behavior at the slits if you chose the screen; and it exhibited after-the-fact particle-like behavior at the slits if you chose the telescopes. Therefore, our delayed choice of how to measure the particle determines how the particle actually behaved at an earlier time.

    How long can we delay the choice? In Wheeler's original thought experiment, he imagined the phenomenon on a cosmic scale, as follows:

1. A distant star emits a photon many billions of years ago.

2. The photon must pass a dense galaxy (or black hole) directly in its path toward earth.

"Gravitational lensing" predicted by general relativity (and well verified) will make the light bend around the galaxy or black hole. The same photon can, therefore, take either of two paths around the galaxy and still reach earth â€" it can take the left path and bend back toward earth; or it can take the right path and bend back toward earth. Bending around the left side is the experimental equivalent of going through the left slit of a barrier; bending around the right side is the equivalent of going through the right slit.

3. The photon continues for a very long time (perhaps a few more billion years) on its way toward earth.

5.  Alternatively, based on what she had for breakfast, our astronomer might choose to use a binocular apparatus, with one side of the binoculars (one telescope) focused exclusively on the left side of the intervening galaxy, and the other side focussed exclusively on the right side of the intervening galaxy. In that case the "pattern" will be a clump of photons at one side, and a clump of photons at the other side.

Now, for many billions of years the photon is in transit in region 3. Yet we can choose (many billions of years later) which experimental set up to employ â€" the single wide-focus, or the two narrowly focused instruments.

We have chosen whether to know which side of the galaxy the photon passed by (by choosing whether to use the two-telescope set up or not, which are the instruments that would give us the information about which side of the galaxy the photon passed). We have delayed this choice until a time long after the particles "have passed by one side of the galaxy, or the other side of the galaxy, or both sides of the galaxy," so to speak. Yet, it seems paradoxically that our later choice of whether to obtain this information determines which side of the galaxy the light passed, so to speak, billions of years ago.

    So it seems that time has nothing to do with effects of quantum mechanics. And, indeed, the original thought experiment was not based on any analysis of how particles evolve and behave over time â€" it was based on the mathematics. This is what the mathematics predicted for a result, and this is exactly the result obtained in the laboratory.

Can we delay the choice even longer? Can we delay the choice until after the photons have "hit" the telescopes or the screen? It turns out we can. We do so with a handy quantum eraser. But that's a whole 'nuther experiment.  See the Delayed Choice Quantum Eraser Commentary.

This is great stuff, isn't it?

Bonus picture!

References:

[1] See Wheeler's "delayed choice", in Quantum Theory and Measurement, edited by J.A. Wheeler and W.H. Zurek, Princeton Univ. Press (1983).

[2] E.g., V. Jacques, et al., "Experimental realization of Wheeler's gedankenexperiment," Science 315 966 (2007), e-print at http://www.arxiv.org/abs/quant-ph/0610241 ; A.G. Zajonc et al., Nature, 353, 507 (1991); P.G. Kwiat et al., Phys. Rev. A 49, 61 (1994); T.J. Herzog et al., Phys. Rev. Lett., 75, 3034 (1995); T.B. Pittman et al., Phys. Rev. Lett., 77, 1917 (1996).  The Jacques experiment is described in Physics World, "Photons denied a glimpse at their observer" (Feb. 15, 2007),  http://physicsworld.com/cws/article/news/27106 .